Beware point estimates of tractability
Published 27 May 2024 ⋅ Comment on EA Forum
Back to writingContents (click to toggle)
6,443 words • 33 min read
Summary: for some problems in the world, efforts towards those problems pay off in a big way only once progress on the problem passes some threshold — once the problem is ‘solved’. We can estimate how much effort is required to solve a given problem, and notice that adding our own effort (or resources) to the status quo would make the difference from “unlikely to solve the problem (in time)” to “likely to solve the problem (in time)”, given that estimate. But often we are very uncertain how much effort is really required to solve the problem, and this matters a lot. The more uncertain we are, the less likely we should think it is that our marginal effort will make the difference between solving and not solving the problem. So in these cases, assuming certainty about the difficulty of a problem would significantly overstate the expected value of working on it, holding other factors fixed. This is a slightly different way of thinking than the ‘ITN’ framework, or at least a way in which ITN is applicable but misleading. This framing could be applicable to problems like open questions in AI alignment, or enacting certain policy change.
The ITN framework
When estimating the usefulness of additional work on a given problem, you can use the ‘importance, neglectedness, tractability’ (ITN) framework. On this framework, the marginal impact of more resources or effort applied to a given problem is the product of those three factors, where:
- Importance =
- Tractability =
- Neglectedness =
So, knowing the I, T, and N of a problem gives us a way to find the marginal impact per marginal resource spent on the problem:
This is true whatever the function of total impact with total resources spent so far looks like, so this bare-bones version of ITN works as a useful definition, but isn’t informative on its own about prospects for future work on a problem. It’s assumption-free.
In his ‘Prospecting for Gold’ talk, Owen Cotton-Barratt suggests a further assumption that the tractability and importance of a problem do not change with total resources spent. This means that the absolute (not marginal) progress on ‘solving’ a problem scales logarithmically with total resources invested:
Since, when and are constants, only logarithmic progress with resources derives to get —
So the marginal impact of resources spent on a problem is proportional to its tractability, whether or not it changes in tractability as progress is made.
But what if we don’t know the values of , , or ? Now we’re in the business of estimating marginal impact, rather than calculating it for sure. But this is easily done. Marginal impact is just the product of the three factors, so if you are uncertain about any one of the factors but certain about the other two, all you need to know is your mean estimate for that factor. Then you just multiply the two known factors with your mean estimate for the unknown factor to get the expected marginal impact of working on that problem.
So, in particular, it doesn’t matter what is the variance or spread of your uncertainty distribution over the true tractability of a problem, if the mean is the same. For instance, the problem of ‘AI alignment’ could turn out to be very easy, or extraordinarily difficult, or somewhere in between — but but matters for estimating the value of work on AI alignment is its expected tractability; the mean of your uncertainty distribution over its tractability.
I think this is technically correct but quite misleading, as I’ll try to explain.
All-or-nothing problems
Some problems are like transferring cash to people in extreme poverty: as long as there are very many people living in extreme poverty, the next 1% of progress toward solving the problem is always roughly as valuable as the previous 1%, even if you knew progress would stop after that next 1%. This is (I think) a natural way to interpret an assumption of constant importance in the ITN framework.
Other problems are more like laying a railway or building a cruiseliner or making a documentary film. If you know that progress will stop sometime before completion, then the next 1% of progress toward completion just isn’t valuable. But you know roughly — say, within a factor of 2 or 3 — the amount of (sidenote: I’ll mostly use ‘effort’ to refer to ‘generic inputs like effort or resources or money’.) required to complete the project.
But some problems are more like how ‘solving Fermat’s last theorem’ might have looked to Pierre Fermat. You know ahead of time that completing 99 of 100 steps sufficient to prove a theorem is far less valuable than completing all 100 steps, if nobody else discovers step 100. But you are also very uncertain how much effort is required to solve the problem in the first place. Perhaps another 6 months of concerted effort could do it. (sidenote: Owen Cotton-Barratt writes: “[These are problems] we only need to solve once (answering a question a first time can be Herculean; answering it a second time is trivial), and which may not easily be placed in a reference class with other tasks of similar difficulty. Knowledge problems, as in research, are a central example: they boil down to finding the answer to a question. The category might also include trying to effect some systemic change (for example by political lobbying).”)
The second two kinds of problem have an all-or-nothing quality in this way: the final few resources spent unlock almost all the potential value accumulated by all previous resource spending (and additional spending beyond that point is either basically worthless or basically nonsensical). But it’s easier to guess how many resources it takes to take some problems or projects to completion, and for others we are stuck with wild uncertainty.
In cases like these, uncertainty matters. Imagine you have a fixed budget totally earmarked for a personal project, and all you care about is completing at least one project. Project A takes a known amount of resources just within your budget, and Project B takes the same expected resources, but with much more uncertainty: it could take significantly fewer or more than your budget. (sidenote: A less vague example: suppose you have a super-8 camera with 10 minutes’ worth of film, and you want to film something cool. One option would be to film Andy perform a 10-minute magic trick routine, which he performs with a 100% success rate. Another option would be to film Beth do a skateboard trick, which takes 1 minute per attempt, and where each attempt has a 10% success rate. A one-minute film of a successful skateboard trick would be just as valuable as a 10-minute film of the magic routine, but 2 skateboard films would be no more valuable. Now, in expectation, both options will require 10 minutes of filming before they pay off. But after 10 minutes, you can be sure to have filmed the magic trick, but you’re only about 65% likely to have filmed a successful skateboard trick.)
But now consider that for big problems in the world — the kind you care about if you care about having lots of impartial impact — you are very rarely the only actor working on the problem. And when you’re one among many actors working on such an ‘all-or-nothing’ problem, you should only expect to be marginally increasing the chance of solving it.
Distributions over effort
Here’s a super simple model of what’s going on when you’re estimating the value of contributing to a globally significant all-or-nothing problem.
Assume you know how much effort will be spent by the rest of the world on solving the problem, and you also know the value of solving the problem, which is constant. Assume all of the value of working on the problem comes from the moment of fully solving it — stopping short delivers no value, and working beyond the solution delivers no value.
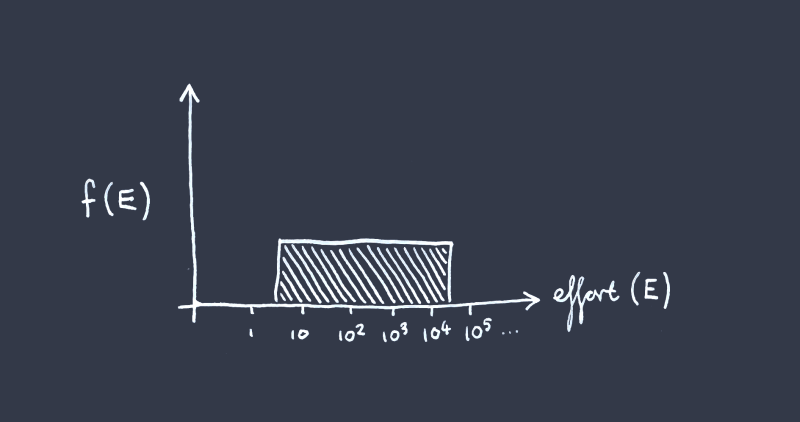
But let’s say you’re uncertain about how much total effort it’s going to require to solve the problem over a few orders of magnitude. In particular, let’s imagine your uncertainty distribution (PDF) over the effort required (sidenote: Why log-uniform? Not because it’s at likely to be the true distribution, but because it locally approximates (around the point of interest, which is on the margin adding to all status quo effort) the kind of distribution you’re going to have for problems of wildly unknown difficulty, that is “cases where we do not have a good idea of the order of magnitude of the difficulty of a task”.
 ) —
) —
Where the anticipated rest-of-world (‘status-quo’) effort falls somewhere within the bounds —
Remember we are trying to estimate the value of adding some amount of additional effort or resources toward solving the problem. In this case, the value of some (sidenote: We’re assuming this is the difference in total effort you cause, accounting for effort you might crowd out or crowd in.) is just the value of solving the problem, multiplied by the area covered by your additional work under the PDF.
Call the lower bound of your log-uniform PDF , and the upper bound . Let stand for the status quo work, which remember falls somewhere within the bounds by stipulation. Then the chance that the problem is solved with only the status quo work (by ) is the fraction of the PDF ‘filled in’ by , which is .
Now let’s imagine you are considering increasing the total work done to . The increase in the chance the problem is solved is then —
Visually, this is just the size of the gap between and as a fraction of the gap between and , viewed on a log scale.
Similarly, the additional chance of success from a marginal unit of additional effort would be, where is the effort spent so far —
Therefore, fixing the amount of status-quo work, the difference your extra work makes is inversely proportional to how wide your uncertainty is over the true difficulty of the problem in log space. This is a very over-simplified but clear model of how uncertainty over the difficulty of an all-or-nothing problem decreases the expected value of contributing to solving it.
In particular, when it is appropriate to be uncertain about the difficulty of a problem in cases like this, it is not safe just to use a point estimate. If you made that mistake, on this model, the expected value of your additional work would be the value of solving the problem just in case your additional work makes the difference on solving it, and zero otherwise. But even if your mean estimate for the difficulty of a problem does fall above the status-quo effort but below the total effort after your contribution, it could easily be inappropriate to expect to make the difference.
Moderate fatalism?
I sometimes hear a case for working on Problem P which sounds like:
It would be a huge deal to solve Problem P in time (great if we succeeded, and/or terrible if failed). But it looks, on our best guess, like the world is currently not on track to solve P; although we’re hopeful a really focused extra push would solve it. So join the push to solve P — basically all the value of solving P is at stake!
In particular, problems around AI alignment can fit this pattern, since they are (sidenote: Either because there are research problems which are clearly either not-solved or solved, or because they are policy or systemic change efforts which clearly either fail or succeed in being enacted.).
I do not think people are basically ever this explicit in making this ‘point estimate of difficulty’ mistake. For most globally important all-or-nothing problems, presumably everyone agrees there is either (i) some chance that the problem gets solved without their help, or (ii) that their help fails to make the difference in solving the problem. So I’m not making a groundbreaking point.
Still, I do think the point sometimes gets a little lost or under-appreciated. That is, (sidenote: The opposite error is also possible, as Owen Cotton-Barratt points out: “if your point estimate is that things will fail even with your extra effort, then things look less bleak if you account for the possible worlds where things are easier than you think and you could actually make the difference.” Therefore, “it’s not always right that point estimates cause people to overstate the value of working on things”.) that they, or the ‘additional effort’ they are part of (like the community they are part of), will make the difference in solving the problem, in particular for big challenges around AI of unknown difficulty.
Often, I think, an appropriate stance to take on such problems is a kind of (sidenote: I might have heard Nick Bostrom use this phrase, but I can’t remember where.), where you think it is (perhaps very) unlikely you will make the difference on solving it in time, but the (perhaps small) contribution you can make to the chance it gets solved still totally justifies your effort.
So is NTI wrong?
The assumption-free version of NTI I outlined at the top can’t be incorrect on its own, because it’s just suggesting a way to decompose marginal impact into factors which are defined so as to multiply up to marginal impact.
Yet, on NTI, it doesn’t matter how wide your uncertainty is over the tractability of a problem, so long as the expected tractability (the mean of your uncertainty distribution over its possible values) stays the same (and holding and fixed). So it sure sounds like I am disagreeing with this feature of NTI. What gives?
Recall that ‘tractability’ is about marginal progress on a problem with marginal resources:
- Tractability =
But it’s up to us to pin down what the ‘problem’ is. For an all or nothing problem, the obvious interpretation would be to measure progress toward the problem (‘% solved’) as progress in terms of the logarithm of effort so far toward the effort toward the logarithm of the total effort required to solve it. If you know the total effort required, then tractability (sidenote: And is equal to ). But the importance of the problem would be zero at every margin short of the point where the problem is solved, recalling:
- Importance =
Another way to measure ‘% solved’ for a problem would be in terms of the % of total achievable impact achieved with the resources so far. Then the tractability of an all-or-nothing problem would be zero at every margin short of the point where the problem is solved.
In both cases, it would be a mistake to only use marginal impact as a guide to action. (sidenote: By contrast, when importance and tractability are constant for a problem, and progress scales sublinearly with effort or resources, then marginal impact is a good guide to action.)
Now consider what happens when you are uncertain ahead of time about how much effort is required to solve an all-or-nothing problem.
Using effort as the measure of progress, this would mean that any expected value of marginal effort would come from the small chance that the next bit of effort solves the problem: the importance of marginal effort is very likely zero, with some chance of being the entire value of (sidenote: You’d also become uncertain about the (constant) value of tractability, but it required zooming out to see how this also influences marginal expected importance.).
Using ‘% of achievable impact achieved’ as the measure of progress, you’d know the importance of progress, but any expected value of marginal effort would come from the small chance that the problem is at all tractable: the tractability of marginal effort is very likely zero, with some chance of being very high at the point where the problem gets solved.
You could also choose to go meta, and change the problem from being the all-or-nothing problem itself, to something like “increase the chance that the problem is solved by ”. The tractability of that problem could be constant, but it wouldn’t be the same thing as your guess at how easy it is to solve the object-level problem — it would be a guess about the difference that additional resources would make.
In fact, I think in all of the cases above, what ITN is calling either ‘tractability’ or ‘importance’ is quite different from what those words intuitively suggest. So ITN isn’t wrong, it’s just awkward for problems like this, or at least demands vigilance against being misled by the terms.
I’d suggest also just making direct estimates of the value of solving a given all-or-nothing problem, and the chance that some extra efforts make the difference on solving it, where intuitive notions of tractability and neglectedness inform your guess on that chance. In particular, if you can imagine angles of attack on the problem, but you have a story for why those angles of attack would be ignored by default, then things look good.
A general limitation of ITN
I think the example I’ve given — where point estimates of problem difficulty fit awkwardly with natural ways of using NTI — point to a more generic limitation of ITN as a method for estimating marginal impact under uncertainty.
The problem is this: suppose you are uncertain about the importance, neglectedness, and tractability of a problem. So for each of I, T, and N, you have a distribution over what value it takes — how much credence you put in any given range for the value it takes. Now, if these distributions were independent, then you could indeed just multiply the expected values of each factor to get a result for the expected marginal impact of working on the problem —
But, crucially, your distributions over each of the factors might easily not be independent, given how the factors are defined.
For example, you might think that a problem’s importance is nonzero only if its tractability is zero, and its tractability is nonzero only if its importance is zero.
To illustrate the general point here, consider a non-marginal example. Suppose a mastermind devises two puzzles: one which is practically impossible (<0.1% likely) to solve in an hour, but whose reward is $1,000; and another which is trivially easy (>99% likely) to solve, but which pays out $1. The mastermind flips a coin to choose a puzzle and places it in a box, so you don’t know which of the two was chosen. You are choosing whether to commit an hour of your time to solving the puzzle in the box, based on the expected reward. What is the expected reward for fully completing the puzzle? $5000.5. What is the expected chance you solve the puzzle? Around evens. Is the expected reward for spending the hour trying to solve the puzzle roughly $2500? Certainly not! In fact, the expected reward is less than $1.
Of course, you can try to think through your joint distribution across I, T, and N —
But two comments here. First, ITN is supposed to be a useful heuristic way to break down the problem of estimating impact. But in these cases where you cannot safely consider the three factors independently from one another, ITN either (i) requires more cumbersome calculation than you’d hope from a heuristic guide (see above); or otherwise (ii) ITN cannot be trusted to deliver the wrong answer (when assuming independence between the factors).
Second, in these cases, the meanings of I, T, and N implied by the framework diverge from common-sense meanings. It doesn’t seem very natural to talk about a problem being conditionally neglected, important, or tractable — as in, “I think this problem is important just in case it is not tractable and vice-versa”.
Appendix
What does the simple model miss?
- The problem you are working on is probably not entirely all-or-nothing: there might be some value to partially solving it, and/or making more progress beyond the most obvious “this problem is now solved” point
- You might not be certain how much effort the rest of the world is going to contribute, ahead of time
- Your uncertainty distribution over the difficulty of the problem (how much effort or resources are required to solve it) might not be log-uniform between bounds (indeed it almost certainly isn’t — this was a convenient simplification)
If anyone wants to extend the model to something more interesting or realistic, that would be great.
Thanks to Phil Trammell for comments.
Relevant reading
- Most problems fall within a 100x tractability range (under certain assumptions) — Thomas Kwa
- How to treat problems of unknown difficulty — Owen Cotton-Barratt
Back to writing